Klíčový rozdíl: kruh a elipsa uzavřely zakřivené tvary. V kruhu jsou všechny body stejně vzdálené od středu, což není případ elipsy; v elipsě jsou všechny body v různých vzdálenostech od středu.
Matematicky, kruh je hlavním tvarem v oblasti geometrie a jeho definicemi: kruh je tvar se všemi body ve stejné vzdálenosti od středu. Jmenuje se podle jeho středu. Některé skutečné příklady kruhu jsou kolečka, večeře a (mince) mince.
Slovo " cirkus " pochází z řeckého výrazu " kirkos ", který je metatezí homerského řeckého a znamená " obruč " nebo " kroužek ". Kruh byl znám před zaznamenanou historií. Slunce a Měsíc jsou přirozeným příkladem kruhu, zatímco i krátká stopka, která fouká ve větru, tvoří tvar písku v kruhu. Princip kruhu byl aplikován při tvorbě kol a převodů předchůdcem. Nyní v moderní době existuje řada strojů založených na kruhovém tvaru. Studium kruhu a jeho vývoj je použitelné v oblastech matematiky, geometrie, astronomie a počtu.
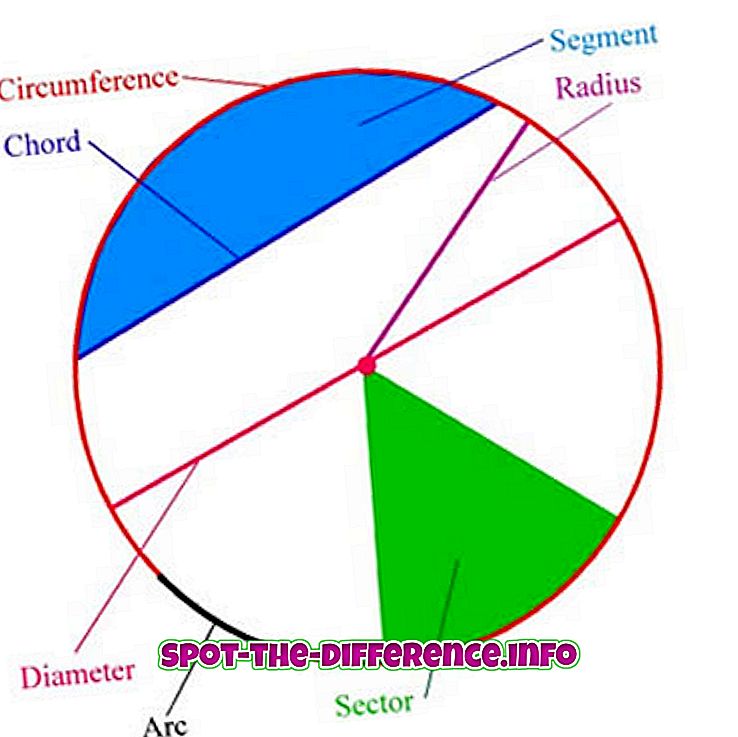
V terminologii kruhu jsou zahrnuty následující pojmy:
Oblouk : jakákoli připojená část kruhu.
Center : bod rovnoměrně od bodů v kruhu.
Poloměr : čárový segment spojující střed kruhu s libovolným bodem samotného kruhu; nebo délku takového segmentu, který má poloviční průměr.
Průměr : čárový segment, jehož koncové body leží na kružnici a prochází středem; nebo délku takového segmentu čáry, což je největší vzdálenost mezi dvěma body v kruhu. Jedná se o zvláštní případ akordů, jmenovitě nejdelší akord, a to je dvojnásobek poloměru.
Obvod : délka jednoho obvodu podél kruhu.
Chord : čárový segment, jehož koncové body leží na kružnici.
Tangent : koplanární přímka, která se dotýká kruhu na jednom místě.
Semicircl e: oblast ohraničená průměrem a obloukem ležícím mezi koncovými body průměru. Je to zvláštní případ kruhového segmentu, a to největšího.
Kruhový sektor : oblast ohraničená dvěma poloměry a oblouk ležící mezi poloměry.
Matematicky, elipsa je společným tvarem v oblasti matematiky. Jeho definice uvádí: zakřivenou čáru tvořící uzavřenou smyčku, kde je součet vzdáleností od dvou bodů (ohnisek) ke každému bodu linky konstantní. Příklady reálného života elipsy jsou: hula obruč, sklenice vody a jednoduchý obličejový talíř, když se nakloní, aby viděli pod úhlem.
Apollonius z Pergy dal jméno "elipsa" v jeho Conics, který zdůrazňuje spojení křivky s aplikací oblastí. Je to křivka v rovině obklopující dvě ohnisková místa tak, že přímka vedená z jednoho z ohniskových bodů do libovolného bodu na křivce a pak zpět k druhému ohniskovému bodu má stejnou délku pro každý bod na křivce. Jeho tvar je reprezentován jeho excentricitou, která je libovolně blízká 1. Studium elipsy a její vlastnosti jsou běžně použitelné v oblasti fyziky, astronomie a inženýrství. Oběžné dráhy planet s Sluncem v jednom z ohniskových bodů, měsíce obíhající kolem planet a další systémy, které mají dvě astronomická těla, jsou obecnými příklady eliptických cest. Tvar planet a hvězd je často dobře popsán elipsoidy. Elipsa je také považována za nejjednodušší postava Lissajous, vytvořená, když horizontální a vertikální pohyby jsou sinusoidy se stejnou frekvencí.
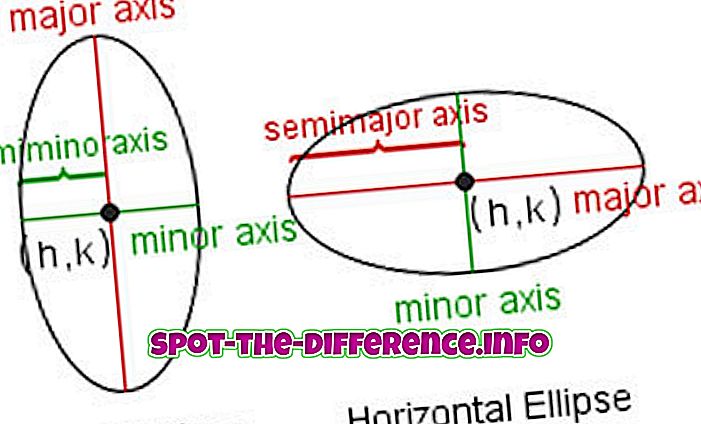
Termíny týkající se zejména terminologie elipsy jsou:
Zaostření : Vzdálenost od středu a je vyjádřena jako hlavní a menší poloměr.
Excentricita : Excentricita elipsy (běžně označovaná jako e nebo ε) je vyjádřena v termínech pomocí zploštělého faktoru.
Directrix : jedná se o přímku rovnoběžnou s vedlejší osou, s níž je spojeno každé zaostření.
Latus rectum : Akordy elipsy, které jsou kolmé k hlavní ose a procházejí některou z jejich ložisek, se nazývají latus konec elipsy.
Hlavní / Menší osa : Nejdelší a nejkratší průměry elipsy. Délka hlavní osy se rovná součtu dvou generátorových linek.
Poloměrná / poloviční osa : Vzdálenost od středu k nejvzdálenějšímu a nejbližšímu bodu elipsy. Polovina hlavní / vedlejší osy.
Akordy : Středy soustavy paralelních akordů elipsy jsou kolineární.
Obvod : souvisí s délkou poloviční osy a excentricitou a je nedílnou součástí elipsy.
Porovnání kružnice a elipsy:
Kruh | Elipsa | |
Definice | Kruh je kulatá rovina, jejíž hranice (obvod) se skládá z bodů rovnoměrně od pevného bodu (střed). | Elipsa je pravidelný oválný tvar, který je vystopován bodem pohybujícím se v rovině tak, že součet jeho vzdáleností od dvou dalších míst (ohnisek) je konstantní, nebo je výsledkem, když je kužel vyříznut šikmou rovinou, což neprotínají základnu. |
Variace | Kruhy se nemění ve tvaru; zůstávají stejným tvarem i při změně pohledu. | Elipsy se mění v tvaru od velmi širokého a plochého až k téměř kruhovitému, v závislosti na tom, jak daleko jsou ohniska od sebe navzájem. |
Konzistence poloměru | Má konstantní poloměr v celém tvaru. | V celém tvaru nemá konstantní poloměr. |
Hlavní součásti | Kruh má jeden poloměr, který leží uprostřed. | Elipsa má dvě ložiska, které jsou na obou koncích. |
Plocha | π × r ^ 2 Kde 'r' je poloměr kruhu. | π × a × b Kde 'a' je délka poloviční osy a 'b' je délka poloměsíčkové osy. |
Standardní rovnice | (xa) ^ 2 + (yb) ^ 2 = r ^ 2 | x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 |
Podobnost | Kruhy jsou jedinečné tvary, ze kterých pocházejí jiné tvary. | Elipsy také vznikají jako obrazy kružnice pod paralelní projekcí a ohraničených případů perspektivní projekce. |