Klíčový rozdíl: Sekvence je uspořádaný seznam čísel nebo pojmů. Může obsahovat prvky, čísla a termíny a může být omezený soubor nebo nekonečný soubor. Série na druhé straně je součtem sekvence.
Série a sekvence jsou nejčastěji slyšeny v matematice a statistikách. Oni také tvoří obrovskou roli ve fyzice, informatice a finance. Ačkoli v angličtině jsou slova vzájemně zaměnitelná, v matematice se definice pořadí a série liší. Sekvence je jednoduše seřazený seznam čísel nebo pojmů. Řada je součtem sekvence.

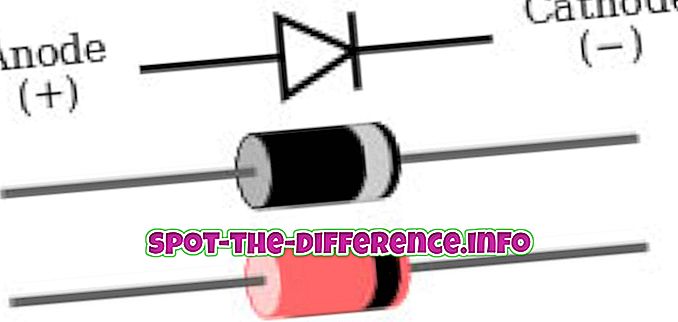
Sekvence je uspořádaný seznam čísel nebo výrazů. Může obsahovat prvky, čísla a termíny a může být omezený soubor nebo nekonečný soubor. Na rozdíl od jedné sady je pořadí v pořadí velmi důležité. Je známá jako diskrétní funkce. Například [1, 2, 3, 4 ...] je sekvence nebo postup (ve Velké Británii). Existují dva typy sekvencí: aritmetická sekvence a geometrická sekvence. Aritmetická sekvence je sekvence, ve které rozdíl mezi dvěma po sobě jdoucími výrazy zůstává konstantní, známý jako společný rozdíl. V geometrické posloupnosti poměr mezi dvěma po sobě následujícími výrazy zůstává konstantní, známý jako společný poměr.
Sekvence mohou být konečné nebo nekonečné, například sekvence všech kladných celých čísel (2, 4, 6 ...). Konečné sekvence jsou někdy známé jako řetězce nebo slova a nekonečné sekvence jako toky. Prázdná sekvence () je zahrnuta ve většině pojmů sekvence, ale může být vyloučena v závislosti na kontextu. Sekvence může být také v přístupu v pořadí nebo sestupném pořadí. Obvykle jde o vzor, který lze snadno vyčíst. Sekvence může být pojmenována nebo označována jako "A" nebo "A n ". Podmínky sekvence jsou běžně pojmenovány jako něco jako "ai" nebo "an", přičemž předepsané písmeno "i" nebo "n" je "index" nebo čítač. Příklad: A2 je druhé místo v sekvenci A6 označuje šest místa v pořadí.

Například součet prvních až desátých termínů sekvence by byl napsán jako

Rovnice může být také napsána v rozšířené podobě jako:
Σ = a1 + a2 + a3 + a1 = 4 + a5 + a6 + a7 + a8 + a9 + a10
Jakákoli písmena mohou být použita jako index, přičemž nejoblíbenějšími jsou i, j, k a n.