Klíčový rozdíl: V matematice se rovnice používá k označení rovnosti mezi dvěma výrazy. Funkce, na druhé straně, je mnohem složitější než rovnice. Funkce se používá k označení vztahu mezi sadou vstupů a sadou odpovídajících výstupů.

Rovnice a funkce jsou dvěma základními základy algebry, předmětem matematiky. Obě mohou být docela složité povahy, nicméně v jejich základní formě mohou být zmateni jako každý jiný. Hlavní rozdíl mezi rovnicí a funkcí je skutečnost, že rovnice se obvykle zabývá jedním vstupem, zatímco funkce může mít mnoho vstupů.

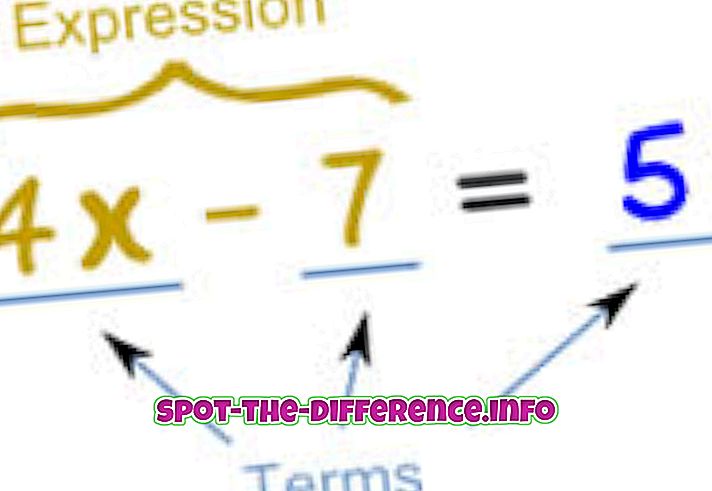
V matematice se rovnice používá k označení rovnosti mezi dvěma výrazy. V podstatě je rovnice napsána jako výraz rovný jinému výrazu. Například: x + 2 = 5. To znamená, že cokoli je x, pokud jej přidáte 2, bude rovno 5. Proto můžeme vyřešit rovnici pro x, která je 3, jako 3 + 2 = 5.

Rovnice mohou být složitější a mohou obsahovat více než jednu proměnnou, jako je x, y, z, atd. V jedné rovnici. Například: 3x + 2y - z = 4. Každou abecedu však bude odpovídat jedno číslo. V tomto případě x = 1, y = 2 a z = 3.

Proto,

3x + 2y - z = 4 se stává

3 (1) + 2 (2) - 3 = 4, což je

3 + 4 - 3 = 4

4 = 4

Funkce, na druhé straně, je mnohem složitější než rovnice. Funkce se používá k označení vztahu mezi sadou vstupů a sadou odpovídajících výstupů. V podstatě by vstup měl dát jediný výstup. Funkce je vztah mezi dvěma proměnnými. Například: f (x) = x + 2. Podle této funkce, cokoliv, vstup je, dá vám jeden výstup, který bude vstup plus 2. Vyřešíme tuto funkci:

Vstup	Funkce	Výstup
X	f (x) = x + 2	f (x)
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

A tak dále…

Funkce mají různé aplikace v matematice, fyzice, informatice atd. Mohou se pohybovat od jednoduché funkce, jak je uvedeno výše, až po složité vzorce nebo algoritmy. Funkci lze považovat za stroj, který poskytuje výstup pro vstup a výstup je nějakým způsobem spojen se vstupem.

Funkce má vždy tři části: vstup, vztah a výstup. Klasický způsob zápisu funkce je "f (x) = ...", kde x označuje vstup a f (x) označuje výstup.

Jak je uvedeno výše, hlavním rozdílem mezi rovnicí a funkcí je, že rovnice má obvykle pouze jeden vstup, který vede k tomu, že výrazy jsou stejné. Zatímco funkce má různé vstupy, z nichž každá dá výstup.